Энэхүү хичээлээр бид квадрат тэгшитгэлтэй холбогдолтой шийдийг олох томьёо, Виетийн терем, квадрат гурван гишүүнтийг үржвэрт задлах талаар авч үзэх болно. 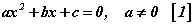 хэлбэрийн тэгшитгэлийг квадрат тэгшитгэл гэдэг. a, b тоонуудыг үл мэдэгдэгчийн коэффициентүүд харин c -г сул гишүүн гэдэг. a≠0 байх
хэлбэрийн тэгшитгэлийг квадрат тэгшитгэл гэдэг. a, b тоонуудыг үл мэдэгдэгчийн коэффициентүүд харин c -г сул гишүүн гэдэг. a≠0 байх 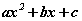 илэрхийллийг квадрат гурван гишүүнт гэнэ.
илэрхийллийг квадрат гурван гишүүнт гэнэ.
Математикийн хичээлийн бүх сэдвийг хамарсан ерөнхий курсын хичээлүүд. Та математикийн хичээлээ давтах, бодлого бодох, шалгалтанд бэлтгэхийн тулд ерөнхий ухагдхуун, үндсэн зарчмуудын талаар тодорхой хэмжээний мэдлэгтэй байх хэрэгтэй. Манай сайтын энэ хэсэгт математикийн хичээлтэй холбогдолтой онолын материалуудыг нийтлэж байх тул эндээс та өөртөө хэрэгтэй мэдээллийг олон авна гэдэгт итгэж байна.
Танд амжилт хүсье.
Нээгдсэн тоо: 45039 Нийтийн
Нээгдсэн тоо: 2667 Бүртгүүлэх
Хувьсах хэмжигдхүүн нь туршилтын үр дүнд тодорхой магадлалтайгаар бодит утга авч байвал түүнийг санамсаргүй гэж нэрлэнэ. Хэрвээ сөрөг биш X хувьсагчийг pi магадлалтайгаар xi утгыг авах харгалзааг тодорхойлох
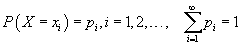
функц байвал X санамсаргүй хэмжигдхүүнийг дискрет гэдэг.
Нээгдсэн тоо: 10506 Нийтийн
Магадлалын аксиом тодорхойлолт
Эгэл үзэгдлүүдийн олонлог E өгөгдсөн ба 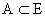 үзэгдэл бүрт :
үзэгдэл бүрт :
- P(A)≥0
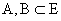 хос харш үзэдлүүдийн хувьд:
хос харш үзэдлүүдийн хувьд: 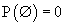 тэнцэл биелнэ,
тэнцэл биелнэ,- P(E)=1
харгалзсан цорын ганц P(A) тоо байна гэж үзье. Тэгвэл E олонлогийн үзэгдлүүдэд магадлал байна. P(A) тоог A үзэгдлийн магадлал гэж хэлнэ.
Нээгдсэн тоо: 9856 Төлбөртэй
Магадлалын онолд үзэгдэл гэдгийг санамсаргүй төгсгөлтэй туршилтаар тохиолдох эсвэл эс тохиолдох дурын үр дүнг ойлгоно. Ийм туршилтын хамгийн энгийн үр дүнг / жишээлбэл зоосон мөнгийг хаяхад тоогоор эсвэл сүлдээрээ унах, хөзөр дундаас нэгийг сугалахад тамга гарч ирэх, шоог хаяхад тодорхой тоо гарч ирэх г.м / эгэл үзэгдэл гэнэ.
Эгэл үзэгдлүүдийн олонлог E -г эгэл үзэгдлийн орон зай гэдэг. Шоо шидэхэд энэ орон зай нь зургаа харин хөзөрөөс карт сугалахад 52 эгэл үзэгдлээс бүрдэнэ. Үзэгдэл нь нэг эсвэл хэд хэдэн эгэл үзэгдлээс бүрдэж болно. Жишээ нь : Хөзрөөс карт сугалахад дараалан хоёр тамга гарч ирэх, шоог гурван удаа хаяхад нэг ижил буух тоо г.м Тэгвэл үзэгдэл гэдгийг эгэл үзэгдлийн орон зайны дурын дэд олонлог гэж тодорхойлж болно.
Нээгдсэн тоо: 5827 Бүртгүүлэх
Олонлогийг латин цагаан толгойн том, элементийг жижиг үсгээр нь тэмдэглэдэг. 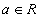 энэ бичлэг нь a нь R олонлогийн элемент ба энэ олонлогт харьяалагдана гэснийг илэрхийлнэ. Эсрэгээр a нь R олонлогт харьяалагдахгүй гэдгийг
энэ бичлэг нь a нь R олонлогийн элемент ба энэ олонлогт харьяалагдана гэснийг илэрхийлнэ. Эсрэгээр a нь R олонлогт харьяалагдахгүй гэдгийг 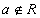 гэж бичнэ.
гэж бичнэ.
Хэрвээ A олонлогийн элемент бүр нь B олонлогт харьяалагддаг эсрэгээрээ B олонлогийн элемент бүр нь A олонлогт харьяалагддаг байвал эдгээрийг тэнцүү олонлогууд (A=B) гэнэ.
Хэрвээ A олонлогийн элемент бүр нь B олонлогт харьяалагддаг бол A олонлог нь B олонлогт багтсан эсвэл A олонлог нь B олонлогийн дэд олонлог гэж хэлдэг. /Зур. 1/ Энэ тохиолдлыг 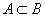 гэж бичнэ. Дурын A олонлогийн хувьд
гэж бичнэ. Дурын A олонлогийн хувьд 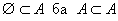 багтаалт хүчинтэй.
багтаалт хүчинтэй.
Нээгдсэн тоо: 3194 Төлбөртэй
Үндсэн ойлголт. Олонлогийн жишээ
Олонлог ба олонлогийн элемент гэдэг нь үгээр утга гаргасан тодорхойлолт байдаггүй суурь ойлголтуудад хамаарагдана. Иймээс тогтсон ерөнхий шинжтэй юмсын цуглуулгын талаар олонлог ба олонлогийн элемент гэсэн яриа үүснэ. Номын сангийн номууд, зогсоол дээрх автомашинууд, тэнгэрийн одод, дэлхийн ургамал амьтны аймаг гэх мэт нь бүгд олонлогийн жишээ юм.
Төгсгөлөг тоотой элементээс бүтсэн олонлогийг төгсгөлөг гэнэ. Жишээ нь: номын хуудас, сургуулийн сурагчид г.м
Нэг ч элементгүй олонлогийг хоосон гэнэ. Жишээ нь: далавчтай заануудын олонлог, sinx=2 тэгшитгэлийн шийдийн олонлог г.м
Нээгдсэн тоо: 5175 Нийтийн
Зарим тодорхой интегралууд
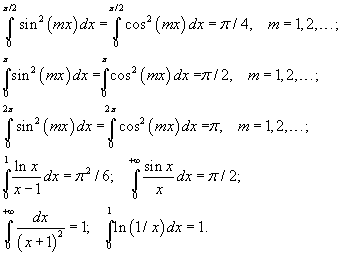
Нээгдсэн тоо: 3092 Нийтийн
Тодорхой интегралыг математик, физик, механик, астроном зэрэг олон салбарт ашигладаг. Бид энд зөвхөн хоёр жишээ авч үзье.
Эргэлдэх биеийн эзэлхүүн
OX тэнхлэг, x=a, x=b шулуунууд, f(x) функцын графикаар хязгаарлагдсан муруй шугаман трапецыг OX тэнхлэгийг тойруулан эргүүлэхэд гарах биетийг авч үзье. /Зур. 10/
Нээгдсэн тоо: 4841 Төлбөртэй
[a,b] хэрчимд өгөгдсөн энэ хэрчимдээ өөрийн тэмдгээ хадгалсан f(x) тасралтгүй функцыг авч үзье. /Зур. 8/ [a,b] хэрчим, x=a, x=b шулуун болон функцын графикаар хязгаарлагдсан дүрсийг муруй шугаман трапец гэдэг. Муруй шугаман трапецын талбайг олохдоо дараах теоремыг ашигладаг.
Хэрвээ f нь [a,b] хэрчимд тасралтгүй, сөрөг биш функц байгаад F нь энэ хэрчимд түүний эх функц нь бол харгалзах муруй шугаман трапецын талбай S нь [a,b] хэрчим дэх эх функцын өөрчлөлттэй тэнцүү.
Нээгдсэн тоо: 4332 Бүртгүүлэх
Хэсэгчлэн интегралчлах.
Хэрвээ u(x) , v(x) функцууд нь тасралтгүй нэгдүгээр эрэмбийн уламжлалтай, 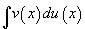 гэсэн интегралтай байвал
гэсэн интегралтай байвал 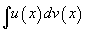 гэсэн интеграл байхаас гадна
гэсэн интеграл байхаас гадна 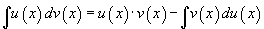 тэнцэл биелж байна. Хураангуй бичлэг нь
тэнцэл биелж байна. Хураангуй бичлэг нь 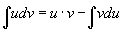 болно.
болно.
Хэсэгчлэн интегралчлах ба үржвэрийн дифференциалууд нь харилцан эсрэг үйлдлүүд гэдгийг сануулъя.





 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.