Геометрийн хичээл математикаас илүү хүнд гэж хүмүүс ярьдаг. Геометрт илүү олон тодорхойлолт, ойлголт, теоремууд орж ирдэгээс үүдэн ингэж үздэг байж болох талтай. Эдгээр нэмэлтүүдийг сайн ойлгоогүй бол геометрийн бодлогыг бодох ямарч боломжгүй. Иймээс Хавтгайн геометр хичээлийн багцыг үзэхийг хичээнгүйлэн зөвлөе.
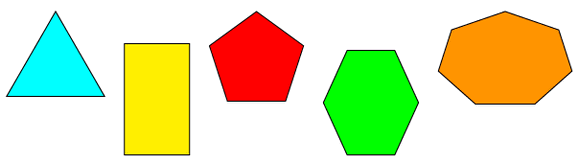
Энэ хичээлд олон өнцөгтүүдийн тухай авч үзье. Огтлолцолгүй битүү тахир шугамаар хязгаарлагдсан геометрийн дүрсийг олон өнцөгт гэнэ.





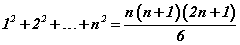
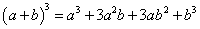 томьёог ашиглан гаргана. Үүнээс санаа аваад өөрөө оролдоод үзээрэй. Чадахгүй бол гаргалгааны дэлгэрэнгүйг үзээрэй.
томьёог ашиглан гаргана. Үүнээс санаа аваад өөрөө оролдоод үзээрэй. Чадахгүй бол гаргалгааны дэлгэрэнгүйг үзээрэй.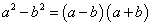 , кубуудын ялгавар
, кубуудын ялгавар 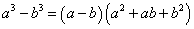 томьёонуудыг ихээр ашигладаг. Тэгвэл дөрөв, тав гэх мэтээр n зэргийн ялгаваруудад тохирох
томьёонуудыг ихээр ашигладаг. Тэгвэл дөрөв, тав гэх мэтээр n зэргийн ялгаваруудад тохирох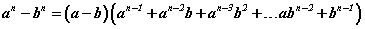
 задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.