Геометрийн ухагдхуунууд практикт ойр боловч сурагчид геометрийн бодлогын нөхцлийг ойлгон зураг гаргаж чадахгүй байх нь элбэг. Энэ нь бодлогын нөхцөлд өгөгдсөн ухагдхууныг зөв ойлгон аваагүйтэй шууд холбоотой асуудал. Иймээс сайтад хавтгайн геометрийн сэдвээр хичээлүүдийг бэлтгэн оруулах санаа төрлөө.

Цэг, шулуун, хэрчим, муруй, өнцөг, хугарсан шугам, тойрог, гурвалжин гэх мэтээр олон төрлийн геометрийн хавтгай дүрсүүд бий.

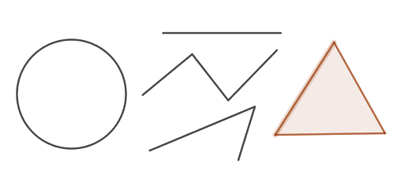
Дээрх зурагт үзүүлсэн дүрсүүдийг сайн ажиглавал эдгээрээс битүү шугамаар үүссэн тойрог, гурвалжин хоёрыг онцолж болохоор.

Шугам гэдэг нь бие биетэйгээ дараалан байрласан цэгүүдийн олонлогоор үүсэх геометрийн дүрс.
Ямар ч шугамыг тодорхой замаар шилжиж буй цэгийн хөдөлгөөний мөр гэж үзэж болно. Жишээ нь цаасан дээр харандаагаар дарвал түүний бал цаасан дээр цэг буюу мөрийг үүсгэнэ. Харандааг цааш цаасан дээгүүр хөдөлгөвөл хөдөлгөөний замаар бал бие биетэйгээ дараалан байрлах цэгүүдийн олонлогийг үүсгэснээр шугам зурагдана.
Геометрийн шугамд өргөн гэсэн ойлголт байдаггүй гэдгийг тогтоон аваарай.

Хавтгайн геометрийн дүрсүүдээс хамгийн өргөн ашигладаг дүрс бол гурвалжин. Гурвалжин түүний чанар, шинж, теоремуудыг сайн ойлгосон байхад ЕБС -ийн геометрийн бодлогуудыг бодоход ихээхэн хөнгөн болдог. Энэ удаа сурагчид сайн мэддэггүй гурвалжны гадаад өнцгийн тухай ойлголтыг танилцуулъя.
Гурвалжны гадаад өнцөг гэдэг нь гурвалжны дурын дотоод өнцөгтэй хамар өнцгийг хэлнэ.

Хавтгайн геометрийг зөв ойлгохын суурь бол түүний үндсэн ухагдхуунуудыг маш сайн ойлгосон байх юм. Үндсэн ухагдхууныг ойлгоогүй бол геометрийн бодлого, асуултыг ойлгон зураг гаргах, асуудлыг шийдэх зэргийг давна гэдэг хэцүү. Хичээлээр хавтгай болон геометрийн дүрсүүд ухагдхууныг авч үзье.

Хавтгай.

Хавтгай гэдэг нь орон зайд тэгш, гөлгөр, бүх тал руу хязгааргүй тархсан гадургуу юм.

Зурагт хавтгайн хэсгийг харуулсан болно.

Олон бодлого бодоод байвал математикт сайжирна гэсэн яриа хүмүүсийн дунд өргөн тархсан байдаг. Бодлого ихээр бодох нь техник талаасаа сайн нөлөөтэй болохоос математикийг ойлгодог болгоно гэдэг эргэлзээтэй. Онолын мэдлэгтэй байх нь ямарч хичээлийн хувьд үндсэн асуудал. Онолгүйгээр хол явахгүй гэж ярьдаг үүнийг хэлж байгаа юм. Энэ удаад Виетийн теоремийн тухай үргэлжлүүлэн авч үзье. Теорем гэдэг нь баталгаа шаардлагатай тодорхойлолт буюу нотолгоо. Өмнөх Виетийн теорем хичээлд жишээ болгон авч үзсэн гурван тэгшитгэлд теорем ажиллаж байгаа ч ямарч тэгшитгэлд адилхан ажиллана гэдгийг батлах хэрэгтэй. Теоремийг нээн олсон математикчид өөрсдөө батлаад түүнийг нь бусад нь хүлээн зөвшөөрсөн учраас математикт теоремоор бүртгэсэн хэрэг. Өнөөг хүртэл жишээ нь Фермагийн их теорем гэдэг нотолгоо батлагдаагүй, олон тооны интегралууд бодогдоогүй байсаар л байгаа. Хүн өөрийн дэвшүүлсэн санаа, нотолгоог баталснаар тэр нь теорем болно.

Хүмүүс математикийг зөвхөн тоотой холбон ойлгодогоос тоо бодлого, тооны хичээл гэж ч ярьж байдаг. Гэтэл тоо бодох нь зөвхөн математикт ч биш бүхий л хичээлд байдаг шүү дээ. Жишээ нь хими, фикик, түүх, газарзүй гэх мэтээр. Тэгэхээр бусад хичээлийн бодлого, тооцоонууд математикийн тооцоо биш болж таарах уу. Мэдээж үгүй бүхий л тооцоо, бодлогод математикийн ухаанд мөрддөг дүрмийг л ашиглана. Математик хүмүүст тоо бодох гэхээсээ илүү хийсвэрлэн сэтгэх, тунгаан бодох, ухан ойлгох чадварыг өгдөг. Иймээс л математикийн ухааныг бүх ухааны хаан гээд байгаа юм. Математикийн бүх зүйлүүд бие биетэйгээ нягт холбоотой, нэг нь нөгөөгөөс урган гардаг учраас буруу, худлаа зүйл байж болдоггүй нь түүнийг нэг талаас амархан нөгөө талаас хүнд хичээл болгодог.

Алгебрын суурь ухагдхууны нэг бол илэрхийллийг хялбарчлах байдаг. Өмнөх хичээлээр рационал бутархай гэж юу болох тэдгээрийг хялбарчилахад үржүүлэхийн хураангуй томьёог хэрхэн ашиглахыг сайн ойлгоогүй бол Рационал бутархайтай ажиллаж сурах I хичээлийг үзэхийг зөвлөе. Бодлого бодох суурь аргачлал илэрхийллийн хялбарчлал дээр тогтдог. Үүнийг сайн эзэмшээгүй үед ямарч бодлого танд хүндрэл үүсгэх бүрэн боломжтой. Иймээс хичээлийг анхааралтай сайн судлан ойлгон авахыг хичээгээрэй.

Нэг үзээд ойлгохгүй бол дахиад үз. Хэн ч таныг олон удаа үзлээ гэхгүй. Интернет сургалтын хамгийн том давуу тал энэ. Зарим хичээлийг үзэхийн тулд багахан төлбөр төлөх хэрэгтэйг Бүртгүүлэх, тусгай эрх нээлгэх нийтлэлээс үзээрэй.

Рационал бутархай гэдэг нь хуваар болон хүртвэр нь олон гишүүнтээс бүрдсэн бутархайг хэлнэ. Монгол хэлний орчуулга гэж байдаггүй байх. Гэхдээ олон гишүүнт хуваар болон хүртвэрт нь орсон бутархайг рационал гээд ойлгоход болно. Рационал бутархайтай ажиллах нь математикийн олон төрлийн бодлогыг бодох үндэс болдог учраас үүнийг сайтар эзэмшсэн байх ёстой. Бутархайг зөв эмхэтгэж сураагүй тохиолдолд энгийн илэрхийллийг ч бодож чадахгүйд хүрдэг. Үүнээсээ болоод сурагчид математикийг хүнд гэж бодон тооны хичээлээс айдаг бүр зугтаадаг болдог. Гэтэл математикийн шинжлэх ухаан нь бусдынхаа суурь тул үүнийг ойлгохгүйгээр өөр бусдад суралцан амжилтад хүрнэ гэдэг бараг мөрөөдөл. Энэ бол миний бодол. Одоо үндсэн асуудалдаа орцгооё.

Модул орсон тэгшитгэл сурагчдыг хүнд асуудалд оруулдаг. Шалгалт шүүлэгт ийм төрлийн тэгшитгэлүүд дээр сурагчид ихэнх нь таах аргаар хариуг бөглөдөг нь нууц биш. Гэтэл тэтэгэлэгт хөтөлбөр, уралдаант шалгалт гэх мэт илүү нарийн авдаг буюу бичгийн шалгалтанд тааж оноо авна гэсэн ойлголт байхгүй болдог. Ялангуяа өгсөн даалгаварын бодолтоор оноо өгдөг бичгийн даалгавар байвал яах билээ. Иймээс сэдвийг онолын болоод практик талаас гүнзгий ойлгосон байх хэрэгтэй. Ингэж чадсан тохиолдолд шалгалт, шүүлэгийг ямарч хэлбэрээр авсан танд асуудал үүсэхгүй. Хичээлээр тэгшитгэлийн хоёр талд модул орсон болон модултай тэгшитгэлийг задлах аргаар бодох тухай үзнэ. Материалыг илүү сайн ойлгохын тулд Модултай тэгшитгэлийг бодох II , Модултай тэгшитгэлийг бодох I хичээлүүдийг үзсэн байхыг зөвлөе. 

ЭЕШ -д 800 оноо, Хоцрогдлыг бүрэн арилгана гэх мэтийн таныг цоо шинэ хүн болгочих юм шиг лоозун бол худлаа зүйл гэдгийг нэг мөр ойлгон аваарай. Таны асуудал таных байхаас өөр хэнийх ч биш тул та өөрөө л хичээн зүтгэн, тэсвэр, тэвчээрээ гаргаснаар амжилтанд хүрнэ гэдгийг хүн төрөлхтний түүх хэзээний баталсан зүйл.

Модултай тэгшитгэлийг бодох I хичээлд модул гэж юу болох, үндсэн томьёоны талаар авч үзсэн. Жишээ болгон энгийн тэгшитгэүүдийг бодсноор модултай тэгшитгэлийг бодох алгоритм байж болох үндэслэлийг гарган ирсэн. Тэгвэл энэ хичээлээр модултай тэгшитгэлүүдийн төрлүүд тэдгээрийг хэрхэн бодох аргачлалд суралцая. Модул ухагдхууныг хүнд гэсэн ойлголтоос болоод сурагчид түүнийг судлан суралцахдаа хойрго хандах явдал бий. Хичээлийн материалыг ойлгохгүй бол дахин үзээд ойлгон авахыг хичээгээрэй. Таныг хичээлийг хэдэн удаа үзсэнг хэн ч мэдэхгүй ямарч зэмлэл, хариуцлага хүлээлгэхгүй, цаг хугацаанд ч шахагдахгүй байдал нь интернет сургалтын давуу тал шүү.