Энэ хичээлээр логарифм тэгшитгэлүүдийг бодох аргуудын талаар авч үзнэ. Хувьсагч утга нь логарифмын тэмдэгт байрлах тэгшитгэлийг логарифм тэгшитгэл гэдэг. Жишээ нь 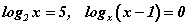
Логарифмын үндсэн адитгал, чанаруудын талаар Логарифм хичээлээс үзээрэй. Үүнээс гадна логарифм тэгшитгэлүүдийг бодож сурахад Үндсэн томьёонуудыг мэддэг байх хэрэгтэй. Логарифм тэгшитгэлийг бодох үндсэн дүрэм бол
Математикийг шинжлэх ухааны хаан гэж зүгээр ч нэг нэрлээгүй юм. Учир нь математик бол шинжлэх ухааны голлох салбаруудын суурь болж байдаг. Математикийг ашигладаггүй салбар гэж байхгүй. Яагаад ерөнхий боловсролын сургуулиудад математикийн хичээлд илүү анхаарал хандуулан заадаг нь үүнтэй холбоотой. Математикт сайн сурагчид бусад хичээлдээ сайн байдаг гэдгийг бүгд мэднэ. Үүний гол нууц нь математик оюун ухаан, сэтгэн бодох, биеэ дайчлах чадварыг хөгжүүлэхэд онцгой нөлөө үзүүлдэгт байгаа юм. Хүн бүр математикч болох албагүй ч энэхүү ухаанд тодорхой хэмжээнд суралцсан байх гарцаагүй шаардлагатай. Хүмүүсийн дунд математикийг их хүнд хичээл ухаантай хүмүүс л сурдаг гэсэн буруу ойлголт их тархсан байдаг. Энэ бол ташаа зүйл шүү. ЕБС-ийн математикийн хөтөлбөр бол хүн бүр мэдэж байж хамгийн анхан шатны суурь ухагдхуун тул хүүхэд бүр сурах бүрэн боломжтой зүйл. Хамгийн гол нь хэдэн үндсэн ойлголтуудыг сайн ойлгосон байхад бусад нь түүнээс дагалдан гардаг учраас магадгүй хамгийн сонирхолтой болоод амархан хичээлүүдийн нэг байж ч мэднэ шүү.
Танд амжилт хүсье
Нээгдсэн тоо: 17040 Нийтийн
Нээгдсэн тоо: 16546 Нийтийн
Алгебрийн тэгшитгэл гэдэгт 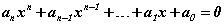 хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая.
хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая.
1. Шугаман тэгшитгэл
n=1 байхад дээрх бичлэг ax+b=0 хэлбэртэй болох бөгөөд ийм төрлийн тэгшитгэлийг шугаман тэгшитгэл гэх бөгөөд дараах аргаар бодно.
- Хэрвээ a≠0, b бодит тоо байвал x=b/a шийдтэй, Жишээ. x-3=2-4x ⇒ x+4x=2+3 ⇒ 5x=5 ⇒ x=1
- Хэрвээ a=0, b=0 бол x дурын тоо байна. Жишээ. 2x+3=5x+5-3x-2 ⇒ 2x-5x+3x=5-2-3 ⇒ 0=0 ⇒ x -дурын тоо
- Хэрвээ a=0, b≠0 бол тэгшитгэл шийдгүй. Жишээ. 2x+1=5x+5-3x-2 ⇒ 2x-5x+3x=5-2-1 ⇒ 0=2 ⇒ шийдгүй.
Нээгдсэн тоо: 2388 Төлбөртэй
Энэ нийтлэлээр элсэлтийн ерөнхий шалгалтын хүрээнд ирдэг тригнометрийн бодлогуудаас арай хүндэвтэр тэгшитгэлүүд, тэдгээрийг бодох аргуудын талаар авч үзэцгээе. Ийм төрлийн тэгшитгэлүүдийг бодож сурах нь танд ямар нэгэн олимпиад, нэмэлт сонгон шалгаруулалтанд /жишээ нь тэтгэлэгт хөтөлбөрт хамрагдах шалгалтууд/ хэрэг болж мэднэ ээ. Та тригнометрийн тэгшитгэлүүдийг бодох стандарт аргуудын талаар эндээс үзээрэй.
Нээгдсэн тоо: 4565 Төлбөртэй
Логарифмыг ердийн тоонуудын адилаар нэмж, хасан төрөл бүрээр хувиргаж болдог. Гэхдээ логарифм бол ердийн тоонууд биш болохоор энд үндсэн чанарууд гэж нэрлэгдэх өөрийн гэсэн дүрэм үйлчилнэ. Эдгээрийг заавал мэддэг байх хэрэгтэй. Үгүй бол логарифмын ямар ч бодлогыг бодох боломжгүй юм. Үндсэн чанарууд олон биш учраас сайн ойлгоод дадлага хийхэд тэдгээрийг тогтоон авахад их цаг хугацаа шаардахгүй. Ингээд логарифмын үндсэн чанаруудтай танилцая.
Нээгдсэн тоо: 2285 Төлбөртэй
Бид илэрхийллийг үржигдхүүнд задлах аргуудын эхний 4 -ийг өмнөх хичээлүүдээр үзсэн. Одоо та квадрат 3-н гишүүнтийг үржигдхүүнд задлахыг бүрэн хэмжээнд сурсан гэж бодож байна. Хэрвээ бид бодлого бодож байхад x -ийн зэрэгт квадратаас /2-оос/ их зэрэгтэй илэрхийлэл ороод ирвэл яах вэ? x -ийн зэрэг хоёроос их илэрхийллийг дээд эрэмбийн гэж нэрлэдэг.
Олон гишүүнтүүд 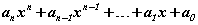 гэсэн ерөнхий хэлбэртэй байдаг. n=1 бол хоёр гишүүнт, n=2 бол квадрат гурван гишүүнт, n>2 их бол ерөнхийд нь дээд эрэмбийнх гэж нэрлээд байгаа хэрэг.
гэсэн ерөнхий хэлбэртэй байдаг. n=1 бол хоёр гишүүнт, n=2 бол квадрат гурван гишүүнт, n>2 их бол ерөнхийд нь дээд эрэмбийнх гэж нэрлээд байгаа хэрэг.
Дээд эрэмбийн олон гишүүнтийн шийдийг олохдоо бид өмнө нь үзсэн аргуудыг ашиглаад үржигдхүүнд задлах боломж гарч болох ч нилээд цаг зарцуулах хэрэгтэй болж мэднэ.
Нээгдсэн тоо: 6676 Төлбөртэй
Логарифм бол ЕБ сургуулийн математикийн хичээлийн хүндхэн сэдэвт ордог. Гэхдээ ерөнхий ойлголтыг зөв авсан байхад сэдэв нь тийм хүнд биш гэдгийг та энэхүү хичээлийг үзээд мэдрэх болно. Гол зүйл бол логарифмын үндсэн тодорхойлолт, түүнийг хэрхэн тооцоход л байгаа юм. Үүнийг сайн ойлгосон байхад цаашид логарифм илэрхийлэл, тэгшитгэл, тэнцэтгэл бишүүдийг бодоход онцын хүндрэл гарах ёсгүй. Логарифмын бодлогуудыг математикийн бүхий л илэрхийлэл, тэгшитгэл, тэнцэтгэл бишүүдийг боддог ерөнхий аргачлалын дагуу тэдгээрийг эхлээд хялбарчлан энгийн хэлбэрт оруулаад эцэст нь үндсэн тодорхойлолтыг ашиглан боддог. За ингээд логарифм гэж юу болохыг ойлгоцгооё.
Нээгдсэн тоо: 3746 Нийтийн
Илэрхийллийг үржигдхүүнд задлах 4 дэх аргад квадрат гурван гишүүнтийг задлах ордог тухай бид Бодлого бодож сурах нь I хичээлд дурдсан байгаа. Бид үржүүлэхийн хураангуй томьёог ашиглан үржигдхүүнд задлах хичээлийн эцэст x2-6x+8 илэрхийллийг бүлэглэх аргыг ашиглан үржигдхүүнд задалсан. Ийм төрлийн илэрхийллийг хэрхэн үржигдхүүнд задлах талаар энэ хичээлээр авч үзэх болно.
Нээгдсэн тоо: 2203 Төлбөртэй
Өмнөх хичээлүүдээр бид ерөнхий үржигдхүүнийг хаалтнаас гаргах, бүлэглэх гэсэн хоёр аргыг сурсан. Энэ удаа үржүүлэхийн хураангуй томьёог ашиглах хүчирхэг аргатай танилцах болно. Үүнийг сурагч бүр мэднэ. Томьёонуудыг ч сайн мэднэ гэж бодож байна. Тэгвэл энэ тухай ярих хэрэг байгаа юм уу гэсэн асуулт гарч болох юм. Томьёонуудыг математикт маш өргөнөөр ашигладаг. Тэдгээрийг үржүүлэх, бутархайг эмхэтгэх, тэгшитгэл бодох, интеграл тооцох гээд хэрэглэхгүй газаргүй. Иймээс эдгээр томьёонууд хаанаас гарч ирсэн, юунд хэрэгтэй, хэрхэн тогтоох, яаж хэрэглэх гээд шуудхан хэлэхэд авч үзэх зүйлүүд байна аа. Сурагчид томьёог сайн цээжилсэн мөртлөө бодлого дээр очоод бараг мэдэггүй хүн шиг болдог. Өөрөөр хэлбэл ашиглах тал дээр ноотой.
Нээгдсэн тоо: 9650 Нийтийн
Прогресстой холбоотой бодлогууд элсэлтийн ерөнхий шалгалтанд ирэх нь бараг уламжлал. Бид энэ хичээлээр прогресстой хамааралтай бодлогуудын талаар авч үзэх болно. Үндсэн ойлголтыг Арифметик ба геометр прогресс хичээлээс аваарай. Прогрессын бодлогуудыг бодоход холбогдох томьёонуудыг мэдэж байхад тийм хүнд биш. Тригнометрийн тэгшитгэл, алгебрийн тэгшитгэл, илэрхийлэл хялбарчлах гэх мэтийн бодлогыг бодох тогтсон аргачлал, дүрэм байдаг бол прогресстой холбоотой бодлогыг бодох тодорхой аргачлалууд гэж байдаггүй бодлогын нөхцөлд тулгуурлан томьёогоо ашиглаад явдаг.
Нээгдсэн тоо: 2618 Төлбөртэй
Элсэлтийн ерөнхий шалгалт дээр тодорхой бус интегралыг олох бодлогууд ирсэн байдаг. Гэхдээ ийм төрлийн бодлого цөөн тооны байдаг ч ЕБС-ийн математикийн хичээлийн программд багтдаг сэдэв учраас тодорхой бус интегралыг бодож чаддаг байх хэрэгтэй. Их дээд сургуулийн эхний курст яг энэ сэдвээр дээд математикийн хичээлүүдтэй тулах учраас хичээлд үзэх аргуудыг мэдэж байх нь шалгалт гэлтгүй цаашдаа хэрэг болно.
Ерөнхий шалгалтын бодлогуудад байгаа тодорхойгүй интеграл олох бодлогууд маш энгийн амархан бараг л хүснэгтийн интеграл байсан гэхэд хилсдэхгүй. Ийм хөнгөн даалгавар дээр сэдвийн аймшигтай нэрнээс сүрдээд оноо алдана гэдэг байж болохгүй.





 задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.