Тригнометрийн хувиргалт, тэгшитгэл, тэнцэтгэл биш гээд тригнометрийн бодлогод хувиргалтын томьёонуудыг өргөнөөр ашигладаг. Эдгээр томьёонууд нилээд олон тооны дээр өөр хоорондоо их төстэй байдаг нь сурагчдыг төөрөгдөлд оруулах явдал ихээр гардаг. Томьёонуудыг цээжилнэ гэвэл нилээд хэцүү тэгээд ч алдах нь гарцаагүй. Энэ хичээлээр хувиргалтын томьёог цээжлэхгүйгээр хэрхэн зөв гаргах талаар авч үзэх болно. Сайн анхааралтай уншаад аргачлалыг тогтоон аваарай.
Хувиргалтын томьёонуудын талаар ярилцахаас өмнө зарим нэгэн ухагдхууны талаар тохиролцох хэрэгтэй. Тэгэхлээр f(x) - гэдгийг sinx, cosx, tgx, ctgx функцуудын аль нэг нь гэе. cof(x) -ээр f(x) функцын кофункцыг тэмдэглэе. Кофункц гэдэг нь синусын хувьд косинус, косинусын хувьд синус харин тангенсийн хувьд котангенс, котангенсийн хувьд тангенс гэсэн үг юм. Илүү ойлгомжтойгоор
Математикийг шинжлэх ухааны хаан гэж зүгээр ч нэг нэрлээгүй юм. Учир нь математик бол шинжлэх ухааны голлох салбаруудын суурь болж байдаг. Математикийг ашигладаггүй салбар гэж байхгүй. Яагаад ерөнхий боловсролын сургуулиудад математикийн хичээлд илүү анхаарал хандуулан заадаг нь үүнтэй холбоотой. Математикт сайн сурагчид бусад хичээлдээ сайн байдаг гэдгийг бүгд мэднэ. Үүний гол нууц нь математик оюун ухаан, сэтгэн бодох, биеэ дайчлах чадварыг хөгжүүлэхэд онцгой нөлөө үзүүлдэгт байгаа юм. Хүн бүр математикч болох албагүй ч энэхүү ухаанд тодорхой хэмжээнд суралцсан байх гарцаагүй шаардлагатай. Хүмүүсийн дунд математикийг их хүнд хичээл ухаантай хүмүүс л сурдаг гэсэн буруу ойлголт их тархсан байдаг. Энэ бол ташаа зүйл шүү. ЕБС-ийн математикийн хөтөлбөр бол хүн бүр мэдэж байж хамгийн анхан шатны суурь ухагдхуун тул хүүхэд бүр сурах бүрэн боломжтой зүйл. Хамгийн гол нь хэдэн үндсэн ойлголтуудыг сайн ойлгосон байхад бусад нь түүнээс дагалдан гардаг учраас магадгүй хамгийн сонирхолтой болоод амархан хичээлүүдийн нэг байж ч мэднэ шүү.
Танд амжилт хүсье
Нээгдсэн тоо: 4365 Төлбөртэй
Нээгдсэн тоо: 12667 Нийтийн
Гурвалжны гайхамшигт цэгүүдээс сурагчдын хамгийн бага мэдээлэлтэй байдаг нь орто төв, орто гурвалжин байдаг. Гэтэл элсэлтийн шалгалт дээр ийм төрлийн бодлогууд ирэх тохиолдол байна. Иймээс энэ хичээлээр гурвалжны орто төв гэж юуг хэлэх түүнийг бодлогод хэрхэн ашиглахыг элсэлтийн ерөнхий шалгалтанд ирж байсан бодлогууд дээр тайлбарлах болно.
Нээгдсэн тоо: 2753 Төлбөртэй
Математикийн элсэлтийн шалгалтанд геометрийн байгуулалт хийх бодлого заавал орж ирдэг. Бодлогууд ихэнхдээ нөхөх хэсэгт ордог бөгөөд зургийг хир зөв гаргаснаас амжилт ихээхэн шалгаалах болно. Нөхөх хэсгийн бодлогын оноо өндөр байдаг. Геомтрийн байгуулалт дээр сурагчид ерөнхий дүрсээ зөв зурсан хэдий ч цаашхи байгуулалт ялангуяа огтлолыг хийхдээ ихээхэн хүндрэлтэй тулдаг. Иймд энэ хичээлээр байгуулалт хийхэд төвөгтэйд орох пирамидын огтлолыг хэрхэн байгуулахыг авч үзэх болно. Сайн зөв зурсан зургаас бодлогын хариуг хэмжээд олчих боломжтой шүү.
Пирамидын огтлолыг байгуулах аргын тодорхой жишээн дээр авч үзцгээе. Пирамидад паралель хавтгайнууд байдаггүй болохоор хавтгайн ирмэгтэй зүсэгч хавтгай огтлолцох шугамыг байгуулахдаа энэхүү ирмэг орших хавтгай дээрх хоёр цэгийг дайрсан шулууныг татах аргыг голдуу хэрэглэдэг.
Нээгдсэн тоо: 7657 Төлбөртэй
Комбинаторикийн бодлогыг бодож сурах хэрэгтэй. Учир нь элсэлтийн ерөнхий шалгалтанд энэ сэдвийн бодлого орж ирэх нь гарцаагүй. Сэдэв өөрөө магадлалын онолын эхлэл болдог тул цаашдаа их дээд сургуульд үзэх хичээлүүдийн суурь тул сайн ойлгосон байх нь чухал. Эхний шатанд сэлгэмэл, гүйлгэмэл, хэсэглэлийн үндсэн томьёонуудын учрыг сайтар ойлгон тэдгээрийг бодлого бодоход хэрхэн яаж хэрэглэхийг сурсан байх шаардлагатай.
 n төрлийн обьект байлаа гэж үзье. Зургийг хар. Энд обьектудыг төлөөлүүлэн ердөө 3 төрлийн дүрсээр жишээ авъя. Эдгээр дүрсүүд дээр сэлгэмэл, гүйлгэмэл, хэсэглэл гэсэн ухагдхууныг авч үзнэ. Нийт обьектын тоо энд нэг их чухал биш гол утга учир ялгааг ойлгох нь чухал. Ухагдхууны ялгааг сайн ойлгоогүйгээс болоод ихэнх сурагчид ийм төрлийн бодлогыг бодохдоо хүндрэлтэй тулдаг.
n төрлийн обьект байлаа гэж үзье. Зургийг хар. Энд обьектудыг төлөөлүүлэн ердөө 3 төрлийн дүрсээр жишээ авъя. Эдгээр дүрсүүд дээр сэлгэмэл, гүйлгэмэл, хэсэглэл гэсэн ухагдхууныг авч үзнэ. Нийт обьектын тоо энд нэг их чухал биш гол утга учир ялгааг ойлгох нь чухал. Ухагдхууны ялгааг сайн ойлгоогүйгээс болоод ихэнх сурагчид ийм төрлийн бодлогыг бодохдоо хүндрэлтэй тулдаг.
Нээгдсэн тоо: 16156 Төлбөртэй
Алгебрийн шугаман тэгшитгэлүүдийн системийг (АШТС) бодоход Гауссын арга их тохиромжтой. Энэ арга бусад аргуудтай харьцуулахад хэдэн давуу талтай.
- Тэгшитгэлийн системийг зохицож байгаа эсэхийг урьдчилан шалгах шаардлагагүй
- Гауссын аргаар тэгшитгэлийн тоо нь үл мэдэгдэгчийн тоотой тохирсон системийг бодож болохын дээр тэгшитгэлийн тоо нь үл мэдэгдэгчийн тоотой тохирохгүй эсхүл үндсэн матрицийн тодорхойлогч тэгтэй тэнцүү системийг ч бодож болдог
- Гауссын арга харьцангуй бага тооцоогоор үр дүнд хүрдэг.
Үндсэн тодорхойлолт ба тэмдэглэгээнүүд
n үл мэдэгдэгчтэй p шугаман тэгшитгэлийн системийг авч үзье. (p болон n тэнцүү байж болно.)
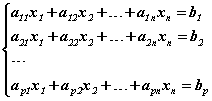
Нээгдсэн тоо: 3454 Төлбөртэй
Тригнометрийн ямарч түвшингийн тэгшитгэлүүд эцэстээ тригнометрийн энгийн тэгшитгэлийн бодолтонд шилждэг. Иймд тригнометрийн энгийн тэгшитгэлийг бодож сурсан байх нь зайлшгүй хэрэгтэй. Энэ үед хамгийн сайн туслах бол тригнометрийн нэгж тойрог байдаг. Синус болон косинусын тодорхойлолтыг санацгаая.
Өнцгийн косинус гэдэг бол нэгж тойрог дээрх тухайн өнцөгт харгалзах цэгийн абсцисс байдаг. Өөрөөр хэлбэл цэгийн OX тэнхлэг дээрх координат юм.
Өнцгийн синус гэдэг бол нэгж тойрог дээрх тухайн өнцөгт харгалзах цэгийн ординат байдаг. Өөрөөр хэлбэл цэгийн OY тэнхлэг дээрх координат юм.
Эдгээр тодорхойлолтыг тригнометрийн энгийн тэгшитгэлүүдийг бодоход хэрхэн ашиглахыг энэ хичээлээр авч үзье.
Нээгдсэн тоо: 8299 Төлбөртэй
Тригнометрийг ойлгох хамгийн энгийн арга бол нэгж тойрог юм. Нэгж тойргийг ойлгосон байхад тригнометрийн хувиргалт, тэшитгэлийг бодоход ашигладаг олон томьёог орлох боломжтой. Зургийг харцгаая.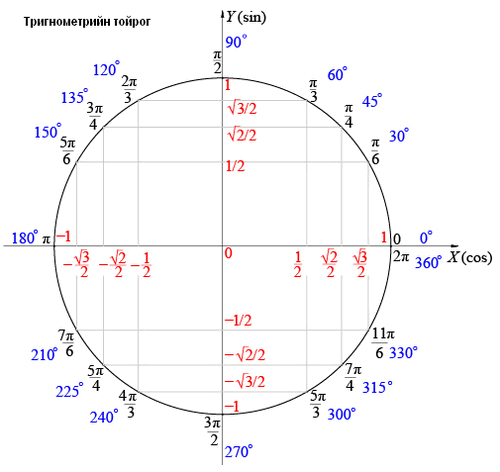
Зургаас бид юуг харах боломжтой вэ?
Нээгдсэн тоо: 2166 Бүртгүүлэх
Арксинус, арккосинус, арктангенс, арккотангенс гэдэг ойлголтоос сурагчид нилээд айдаг. Эдгээр ухагдхууныг сайтар ойлгоогүйн улмаас түүнийг ашиглах, тэдгээртэй холбогдолтой бодлого бодохоос зайлсхийдэг. Өөрөөр хэлбэл айнаа л гэсэн үг. Гэхдээ эдгээр нь ойлгосон хүндээ тригнометрийн тэгшитгэлийг бодоход асар тус болдог энгийн л ойлголтууд гэдгийг та энэ хичээлийн эцэст мэдэн авах болно.
Синус, косинус, тангенс, котангенс талаар мэдэж байхад илүүдэхгүй. Тэдгээрийн зарим өнцгүүдийн утгууд гээд хамгийн ерөнхий зүйлийг мэдэж байхад асуудал үүсэхгүй ойлгоно.
Нээгдсэн тоо: 8979 Нийтийн
Тэгш өнцөгт гурвалжин дахь порпорционал хэрчмүүдийн хоорондын харьцааг тогтоон авах нь их хэрэгтэй. Тэгш өнцөгт гурвалжны гипотенузэд буулгасан өндөр түүнийг катетуудын проекц гэж нэрлэгдэх хэрчмүүдэд хуваадаг.
Тэгш өнцөгт гурвалжны шинжүүд
- Гипотенузэд буулгасан өндөр нь гипотенуз дээрх катетуудын проекцуудын дундаж порпорционалтай тэнцүү.
- Катет нь гипотенуз ба энэхүү катетын гипотенуз дээрх проекцын дундаж порпорционалтай тэнцүү.
Нээгдсэн тоо: 7105 Төлбөртэй
Бодлогын нөхцөлд трапецид багтсан тойрогийн талаар дурдсан бол бодолтын санаагаа дараах шинжүүдийг үндэслэн хийж байгаарай. Үүнд:
1. 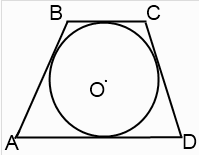 Дөрвөн өнцөгтийн эсрэг орших талуудын нийлбэр тэнцүү байхад л түүнд тойргийг багтааж болдог. Эндээс трапецид тойрог багтсан гэвэл түүний сууриудын нийлбэр хажуу талуудын нийлбэртэй тэнцүү байна.
Дөрвөн өнцөгтийн эсрэг орших талуудын нийлбэр тэнцүү байхад л түүнд тойргийг багтааж болдог. Эндээс трапецид тойрог багтсан гэвэл түүний сууриудын нийлбэр хажуу талуудын нийлбэртэй тэнцүү байна.
AB+CD=AD+BC





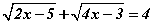 тэгшитгэл бод.
тэгшитгэл бод.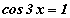 тэгшитгэл бод.
тэгшитгэл бод.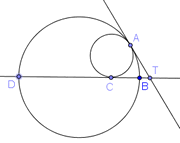 Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.