x2=a гэсэн дутуу квадрат тэгшитгэлийг авч үзье. Энд a - тодорхой тоо. Энэ тэгшитгэлийн шийд нь
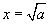 болно.
болно.
Энд гурван тохиолдол гарна.
1. Хэрвээ a=0 бол x=0
2. Хэрвээ a нь эерэг тоо бол тэгшитгэл эерэг, сөрөг хоёр шийдтэй.
Жишээ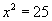 тэгшитгэл нь 5, -5 гэсэн хоёр шийдтэй. Шийдийг дараах хэлбэрээр
тэгшитгэл нь 5, -5 гэсэн хоёр шийдтэй. Шийдийг дараах хэлбэрээр 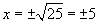 гэж бичдэг.
гэж бичдэг.





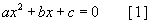
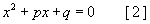
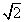
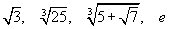
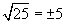 Учир нь (+5)2=25 бас (-5)2=25 байдаг.
Учир нь (+5)2=25 бас (-5)2=25 байдаг. 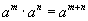
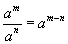
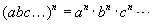
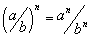
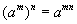
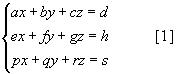 хэлбэрийн тэгшитгэлийн системийг
хэлбэрийн тэгшитгэлийн системийг 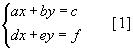 хэлбэрийн тэгшитгэлийн системийг
хэлбэрийн тэгшитгэлийн системийг 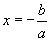
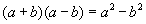 үсгэн тэнцэл нь бас адитгал. Учир нь үсгүүдийн бүх утганд тэнцэл биелнэ.
үсгэн тэнцэл нь бас адитгал. Учир нь үсгүүдийн бүх утганд тэнцэл биелнэ.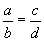 порпорцоос ad=bc / диагнолд байрлах гишүүдийн үржвэр тэнцүү / гарна. Мөн түүнчлэн ad=bc тэнцлээс дараах порпорцууд гарна.
порпорцоос ad=bc / диагнолд байрлах гишүүдийн үржвэр тэнцүү / гарна. Мөн түүнчлэн ad=bc тэнцлээс дараах порпорцууд гарна.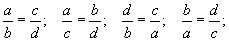
 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.