Бод эсвэл хүүгээр өрсөлдөгчийн хоёр шатарт зэрэг довтлохыг давхар дайралт гэнэ. Тухайн тохиолдол болох гурван шатарт зэрэг дайралт хийх нь практикт ховор байдаг. Давхар дайралт нь хамгийн өргөн дэлгэрсэн тактикийн арга бөгөөд энэ арга хэрэглэгдээгүй нэг ч өрөг байдаггүй гэвэл бараг хэтрүүлэг болохгүй. Арга нь өргийн аль ч үед дайралдаж болохоос гадна түүнийг бүх шатрууд (ноён хүртэл) хэрэгжүүлж чаддаг. Бэрс, морь нь энэхүү тактикийн аргыг хамгийн үр дүнтэй гүйцэтгэгчид болно. Бэрс болон морины цохилт найман зүгт үйлчилдэг тул үүнд гайхах зүйлгүй. Бэрс нь хөлгийн бараг хагасыг хяналтандаа авч чадах хамгийн хүчтэй бод харин морь өөрийн болон хүний шатар дээгүүр даван нүүдэг онцлогтой. Хүү болон мориор хийгдэж байгаа давхар цохилтыг шатрын номуудад ац гэж нэрлэдэг.
Шатар бол оюуны гимнастик гэдэг. Иймээс хүн бүр шатарчин болох албагүй ч энэхүү гайхамшигтай тоглоомыг тоглож чаддаг байх нь чухал. Ялангуяа хүүхэд багачууд шатар тоглож сурах нь тэдний сурлага, хүмүүжилд их сайн нөлөө үзүүлдэг тул манай ЕБС-ийн хичээлийн программд шатрын хичээлийг оруулахаар болсон байх. Гэхдээ шатрыг заавал багшаар заалгах албагүй. Өөрөө сурах бүрэн боломжтой. Яг тогтсон тодорхой дүрэмтэй тул буруу сурна гэсэн ойлголт байхгүй. Шатраар тууштай хичээллэж амжилт гаргахын тулд танд бүр хувийн дасгалжуулагч багш хэрэгтэй болно. Анхан шатны мэдлэгийг өөрөө сурахад ямарч асуудалгүй.
Танд амжилт хүсье
Нээгдсэн тоо: 14289 Нийтийн
Сайн шатарчин болохыг хүссэн хэн болгон сайн стратегч тактикч байх ёстой. Энэ юу гэсэн үг вэ? Юуны өмнө шатарчин шатрын хөлөг дээр тулаан явуулах стратегийн болон тактикийн төрөл бүрийн аргуудыг эзэмшин тэдгээрийг сайн ашиглаж сурсан байх хэрэгтэй. Шатар тоглохдоо төлөвлөгөөтэй байхыг бид олон удаа сануулж байсан. Шатрын өргийн тулаан гэдэг нь өрсөлдөгч нарын төлөвлөгөөний тулаан юм. Өрсөлдөгч бүр эсрэг талынхаа санаанд саад болон өөрийн төлөвлөгөөг хэрэгжүүлэхийг хичээнэ. Тэмцлийн чиглэл, тулааны төлөвлөгөө боловсруулах нь шатрын стратегийн үндсэн асуудал болно. Стратег төлөвлөгөөний хэсэгчилсэн асуудлыг шийдвэрлэхэд тактик хэрэгтэй. Зарим тохиолдолд тактик нь эцсийн зорилгод хүрэх тэмцэлд бие даасан үүрэг гүйцэтгэж болдог.
Нээгдсэн тоо: 2971 Нийтийн
Өмнөх хичээлүүдээр бид шатрын гурван үеийн талаар тус тусд нь дэлгэрэнгүй авч үзсэн билээ. Одоо бид тулаан шатрын гурван үеийг дамжин өрнөх бүтэн өргийг авч үзэх болно. Энэ нь уншигч танд эдгээр үеүүдийн хоорондын уялдаа холбоог олон хараж дадлагажих боломжийг олгох юм.
Франц хамгаалалт
Нимцович - Дурас
Сан-Себастьян, 1912
Нээгдсэн тоо: 3860 Нийтийн
Шатрын тоглолтын нүүдлүүд хугацаагаар хэмжигдэнэ. Ижил тооны нүүдэлд хэн нь олон шатрыг тулаанд оруулсан тал нь хугацааны давуу талыг олж авдаг. Гарааны үндсэн зарчмуудын нэг болох бодоо хурдан хөллөх зарчимыг зөрчвөл өрсөлдөгч талд санаачлагыг алдан өөрөөр хэлбэл нөгөө талыг хугацааны давуу байдалтай болгоно. Гарааны зарчмуудын талаарх хичээлүүдийг дахин сайтар үзэхийг зөвлөж байна. Хичээлүүдэд гарааны зарчмыг умартан өөр зүйлд хэт анхаарсанаас болоод шатарчид хэрхэн бут ниргүүлж байгааг үзүүлсэн сургамжтай өргүүдийг авч үзсэн. Уншигч танд дараах бас нэгэн сургамжтай өргийг толилуулъя.
Нээгдсэн тоо: 1578 Төлбөртэй
Өмнөх хичээлийн 2-р диаграмд үзүүлсэн байрлалд хөлгийн ихэнх хэсэг цагаан шатруудын хяналтанд орсон тул тэдний хөдөлгөөн их чөлөөтэй байсан. Энэ нь тэдний газар нутгийн давуу талыг тодорхойлно. Иймэрхүү давуу байдал нь удаан хугацааны байдаг учраас бүх тулаанд амжилт гаргаж болно гэж тооцож болно. Хүүний массиваар дэмжүүлэн илүү газар нутгийг (талбай) эзлэх тусмаа давуу тал илүү тогтвортой болно. Хүүний гинж нь эсрэг талын боднуудын хэсэг тэр ч бүү хэл бүгдийнх нь үйл ажиллагааг саармагжуулахад их үр дүнтэй. Аль нэг тал нь хөлгийн ихэнх хэсгийг эзлэн авснаар эсрэг талын хүчнүүд хөдөлгөөний хувьд хязгаарлагдах нь ойлгомжтой.
Нээгдсэн тоо: 3537 Нийтийн
Шатарт материалын болон байрлалын гэсэн хоёр төрлийн давуу байдал байдаг. Ямарч шатарчин заавал туулан гардаг шатар тоглох чадварт суралцах эхний үе бол харилцан солилцоо хийж сурах юм. Энэ нь материалын (хүчний) давуу (бод илүү, хүү илүү, илүү хүчтэй бод сул бодны эсрэг гэх мэт) талтай нягт уялдаатай. Энд хүртэл бидний үзсэн хичээлүүд энэхүү шатрын үндсэн элементүүдийн нэгийг нээн ойлгоход зориулагдсан болно. Тэгээд ч бид цаашдаа материалын давуу талаа хэрхэн ашиглах аргуудыг олон удаа авч үзнэ. Материалын давуу талаа чадварлаг ашиглах нь ямарч шатарчны ур чадварын үндсэн бүрдүүлэгч байдаг тухай бид нэг бус удаа дурдаж байсан.
Нээгдсэн тоо: 2481 Төлбөртэй
Бид захын хүүнүүд хичээлд түлхүүр нүдний тухай ойлголттой танилцсан. Эдгээрийг эзлэн авах нь шатрын тулааны эцсийн үр дүнд нөлөөлдөгийг бид мэднэ. Захын биш нүүргүй хүүнд бас түлхүүр нүднүүд гэж байдаг. Захын биш хүүнүүд нэг биш гурван түлхүүр талбартай байдгаараа захын хүүнээс ялгаатай.
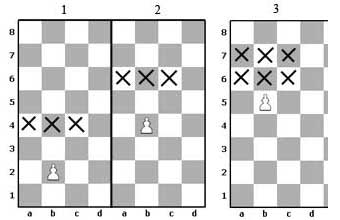 |
1-р диаграмд b2 нүдний хүүний түлхүүр талбаруудыг Х тэмдгээр үзүүлсэн. Эдгээр талбаруудад a4, b4, c4 нүднүүд орно. Хүү урагшаа давшихад түүний түлхүүр талбарууд даган хөдөлнө. b4 хүүний хувьд (2-р диаграм) түлхүүр талбарууд нь a6, b6, c6 болох жишээтэй. Хүү дундаж шугамыг өнгөрөхөд түүний түлхүүр талбар (a6, b6, c6, a7, b7, c7) 6 болдог. (3-р диаграм) |
Нээгдсэн тоо: 2707 Төлбөртэй
Өмнөх хичээлийн жишээнүүдээс дүгнэн үзвэл захын хүүг бэрс гаргахад хамгаалж байгаа тал боломж ихтэй байсан. Тэгвэл илүү хүү нь захын биш байрлалтай бол байдал хэрхэн өөрчлөгдөх вэ? Хүчтэй тал өөрийн төлөвлөгөөг биелүүлж чадах уу? Захын хүүнүүд хичээлийн 2-р диаграмд хамгаалж байгаа талын ноён хүүний замд саад хийж чадахааргүй тохиолдолд асуудал амархан шийдэгдэж байсан. Тэгвэл хүүний давшиж байгаа босоо шугамд эсрэг ноён зогсож байгаа бол юу болох вэ? Дараах жишээнүүдээр дээрх асуултуудад хариулт өгөхийг оролдоё.
Юуны өмнө 1-р диаграмд анхаарна уу.
Нээгдсэн тоо: 1714 Төлбөртэй
Квадратын дүрэмийн тухай 2 хичээлд үндсэндээ хүү өөрийн шатруудын тусламжгүйгээр бэрс гарах оролдлого хийх талаар үзсэн. Практикт нүүргүй хүүнд өрсөлдөгч тал саад болох нь тодорхой тул түүнд өөрийн ноёны тусламж ихэнхдээ шаардлагатай болдог. Тухайн тохиолдол бүрд хүүнд тусламж хэрэгтэй эсэхийг тогтоох нь ойлгомжтой.
Ноёнгоор нүүргүй хүүд туслах үндсэн арга нь хүүний давшиж байгаа шугам ялангуяа бэрс гарах нүднээс эсрэг ноёнг шахах юм. Өөрөөр хэлбэл хоккей, хөл бөмбөгт тоглогчид шайб болон бөмбөгний төлөө тэмцдэгийн адилаар манай ноён өрсөлдөгч ноёнтой мөр мөрөөрөө түлхэлцэхтэй ижил. Жишээ авч үзье.
Нээгдсэн тоо: 2317 Төлбөртэй
Квадратын дүрэм нь практикт их хэрэг болдог тул түүнийг сайн эзэмших шаардлагатай. Илүү нарийн байрлалд дүрэм туслах нь элбэг.
 |
И. Бергерийн сургалтын байрлалд (1-р диаграм) цагаан 1. Тр:b6+ Б:b6 2. Б:f6+ Нc5 гэж нүүн хүүний эндшпильд шилжвэл бэрсээ солилцохоос үл хамааран гарцаагүй тэнцээгээр дуусах болно. Харин цагаан 1. Б:f6+ Б:f6 2. Тр:b6+ Нe5 3. Тр:f6 Н:f6 4. b6 гэж нүүвэл хар ноён хүүний квадратын гадна үлдэх тул цагаан хожих болно. |





 тэгшитгэлийг бод.
тэгшитгэлийг бод.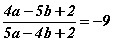 бол
бол 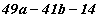 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.