
Алгебр сэдэв орж ирэхэд сурагчдад томоохон асуудал үүсдэг. Тоон дотор үсэг орж ирэх нь сурагчдад багагүй хүндрэлийг дагуулдагаас үүдэн математикт дургүй, сонирхолгүй болох хүнд хэцүү гэсэн ойлголтыг төрүүлэх тал бий. Тоон доторх үсэг бас тоо гэдгийг эхнээс нь зөв ойлгуулбал хэцүү зүйл ердөө байхгүй. Сурагчдад үүсдэг энэхүү хүндрэлийг бага ч гэсэн хөнгөвчлөх үүднээс алгебрийн хичээлийн багцыг нийтэллээ. Хичээлүүд ойлголт бүрээр бага хэмжээтэй тул танд онцын ачаалал өгөхгүй бөгөөд багшийн заасан зүйлийг бататган ойлгон авахад туслана.
Хүүхдүүд олон тоо бодвол математикт сайн болно гэж боддог бололтой. Үнэндээ суурь ойлголтыг мэдэхгүй бол ямарч тоог бодох боломжгүй тул эхлээд онолын суурь мэдлэгийг заавал эзэмших хэрэгтэй. Тоонууд хязгааргүй ч боддог аргачлалууд тийм олон биш учраас эхлээд бодох аргачлалаа сураад дараа нь түүний хэрэглэгээг тоо бодох замаар бататгах хэрэгтэй. Түүнээс хэн нэгний бодсон эсхүл бодолт хийж байгааг хуулаад тоо бодож сурахгүй гэдгийг байнга санаарай.
Зарим хичээлүүд төлбөртэй тул та хичээлүүдийг бүгдийг үзэхийн тулд Тусгай эрхтэй хэрэглэгч байх ёстойг анхаарна уу.
Танд амжилт хүсье.





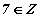 бичлэгийг "5 нь Z олонлогт харьяалагдана" эсхүл "5 нь Z олонлогийн элемент" гэж уншина.
бичлэгийг "5 нь Z олонлогт харьяалагдана" эсхүл "5 нь Z олонлогийн элемент" гэж уншина.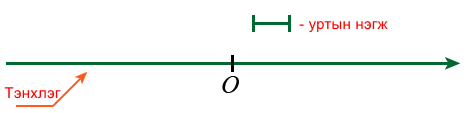
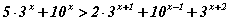 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.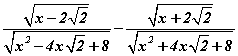 илэрхийллийн x=3 утгыг ол.
илэрхийллийн x=3 утгыг ол.