Шатарт материалын болон байрлалын гэсэн хоёр төрлийн давуу байдал байдаг. Ямарч шатарчин заавал туулан гардаг шатар тоглох чадварт суралцах эхний үе бол харилцан солилцоо хийж сурах юм. Энэ нь материалын (хүчний) давуу (бод илүү, хүү илүү, илүү хүчтэй бод сул бодны эсрэг гэх мэт) талтай нягт уялдаатай. Энд хүртэл бидний үзсэн хичээлүүд энэхүү шатрын үндсэн элементүүдийн нэгийг нээн ойлгоход зориулагдсан болно. Тэгээд ч бид цаашдаа материалын давуу талаа хэрхэн ашиглах аргуудыг олон удаа авч үзнэ. Материалын давуу талаа чадварлаг ашиглах нь ямарч шатарчны ур чадварын үндсэн бүрдүүлэгч байдаг тухай бид нэг бус удаа дурдаж байсан.
Төрөл бүрийн сэдвээр нийтлэгдсэн хичээл, материалуудыг энэ хэсэгт нийтэлсэн юм. Та өөрийгөө хөгжүүлэх, бие даан суралцах эрмэлзлэлтэй байхад эндээс хэрэгтэй зүйлийг судлан мэдэх боломжтой. Интернет ашиглан бие даан суралцах нь орон зай, цаг хугацаанаас хамааралгүй хамгийн хямд, энгийн, үр дүнтэй арга. Ийм төрлийн сургалт өнөөдөр боловсрол олгох хэмжээнд хүртэл хөгжсөн гэдгийг та мэдэх байх. Хамгийн гол нь суралцагч өөрөө идэвхи санаачлагатай байх хэрэгтэй. Энэ нь хүн өөрийгөө хянан, дайчилж сурахад хамгийн их тус нэмэр болж байгаа юм даа. Та оролдоод үз. Бүгд болох ёстой.
Танд амжилт хүсье.
Нээгдсэн тоо: 2465 Төлбөртэй
Бид захын хүүнүүд хичээлд түлхүүр нүдний тухай ойлголттой танилцсан. Эдгээрийг эзлэн авах нь шатрын тулааны эцсийн үр дүнд нөлөөлдөгийг бид мэднэ. Захын биш нүүргүй хүүнд бас түлхүүр нүднүүд гэж байдаг. Захын биш хүүнүүд нэг биш гурван түлхүүр талбартай байдгаараа захын хүүнээс ялгаатай.
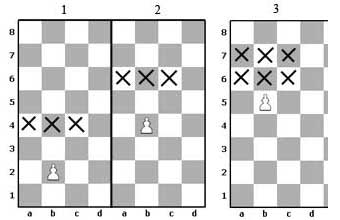 |
1-р диаграмд b2 нүдний хүүний түлхүүр талбаруудыг Х тэмдгээр үзүүлсэн. Эдгээр талбаруудад a4, b4, c4 нүднүүд орно. Хүү урагшаа давшихад түүний түлхүүр талбарууд даган хөдөлнө. b4 хүүний хувьд (2-р диаграм) түлхүүр талбарууд нь a6, b6, c6 болох жишээтэй. Хүү дундаж шугамыг өнгөрөхөд түүний түлхүүр талбар (a6, b6, c6, a7, b7, c7) 6 болдог. (3-р диаграм) |
Нээгдсэн тоо: 2655 Төлбөртэй
Өмнөх хичээлийн жишээнүүдээс дүгнэн үзвэл захын хүүг бэрс гаргахад хамгаалж байгаа тал боломж ихтэй байсан. Тэгвэл илүү хүү нь захын биш байрлалтай бол байдал хэрхэн өөрчлөгдөх вэ? Хүчтэй тал өөрийн төлөвлөгөөг биелүүлж чадах уу? Захын хүүнүүд хичээлийн 2-р диаграмд хамгаалж байгаа талын ноён хүүний замд саад хийж чадахааргүй тохиолдолд асуудал амархан шийдэгдэж байсан. Тэгвэл хүүний давшиж байгаа босоо шугамд эсрэг ноён зогсож байгаа бол юу болох вэ? Дараах жишээнүүдээр дээрх асуултуудад хариулт өгөхийг оролдоё.
Юуны өмнө 1-р диаграмд анхаарна уу.
Нээгдсэн тоо: 1699 Төлбөртэй
Квадратын дүрэмийн тухай 2 хичээлд үндсэндээ хүү өөрийн шатруудын тусламжгүйгээр бэрс гарах оролдлого хийх талаар үзсэн. Практикт нүүргүй хүүнд өрсөлдөгч тал саад болох нь тодорхой тул түүнд өөрийн ноёны тусламж ихэнхдээ шаардлагатай болдог. Тухайн тохиолдол бүрд хүүнд тусламж хэрэгтэй эсэхийг тогтоох нь ойлгомжтой.
Ноёнгоор нүүргүй хүүд туслах үндсэн арга нь хүүний давшиж байгаа шугам ялангуяа бэрс гарах нүднээс эсрэг ноёнг шахах юм. Өөрөөр хэлбэл хоккей, хөл бөмбөгт тоглогчид шайб болон бөмбөгний төлөө тэмцдэгийн адилаар манай ноён өрсөлдөгч ноёнтой мөр мөрөөрөө түлхэлцэхтэй ижил. Жишээ авч үзье.
Нээгдсэн тоо: 2287 Төлбөртэй
Квадратын дүрэм нь практикт их хэрэг болдог тул түүнийг сайн эзэмших шаардлагатай. Илүү нарийн байрлалд дүрэм туслах нь элбэг.
 |
И. Бергерийн сургалтын байрлалд (1-р диаграм) цагаан 1. Тр:b6+ Б:b6 2. Б:f6+ Нc5 гэж нүүн хүүний эндшпильд шилжвэл бэрсээ солилцохоос үл хамааран гарцаагүй тэнцээгээр дуусах болно. Харин цагаан 1. Б:f6+ Б:f6 2. Тр:b6+ Нe5 3. Тр:f6 Н:f6 4. b6 гэж нүүвэл хар ноён хүүний квадратын гадна үлдэх тул цагаан хожих болно. |
Нээгдсэн тоо: 3405 Нийтийн
Урт хугацааны олон нүүдэлт тэмцлийн эцэст аль нэг тал нь нэг хүүний давуутай хүүний эндшпильд орох нь цөөнгүй байдаг. Ийм багахан хэмжээний материалын давуу тал ялалтанд хангалттай юу? гэсэн асуулт гарч ирнэ. Хүүний төгсгөлийг тоглох зарчим дүрмүүдийг сайтар судалж байж л энэхүү асуултын хариуг олох болно. Юуны өмнө хамгийн бага материалын давуу тал болох ноён ганц хүүтэйгээр ноёны эсрэг хэрхэн тоглохыг эзэмших хэрэгтэй. Онолоор хүчний ийм харьцаа бүхий байрлал 160 гаруй мянгаар тоологдоно. Ийм хязгааргүй далайд хэрхэн баримжаалах вэ? Үнэндээ бол үүний тулд энгийн 2-3 дүрмийг мэдэж байхад л хангалттай.
Нээгдсэн тоо: 1624 Төлбөртэй
Материалын давууг ашиглах I хичээлийн 7-р диаграмын жишээ нь их хэмжээний материалын давуу талтай (хөнгөн бодны илүү) хэдий ч энэхүү давуу байдлаа ашиглахад тодорхой хэмжээний техникийн хүндрэл гардаг гэдгийг гэрчилж байна. Үүнээс гадна зэрэглэл багатай шатарчид ч гэлтгүй мастеруудын практикт дээрх техникийн хүндрэлийг давах нь нилээд хүндхэн асуудлыг бий болгодог.
1-р диаграмд үзүүлсэн байрлалд өндөр зэрэглэлийн шатарчин А.Нимцович хүртэл ялалтанд хүрэх зөв замаа олоогүй байдаг.
Нээгдсэн тоо: 1654 Төлбөртэй
Доогуур зэрэглэлийн болон эхлэн суралцагчид хооронд тоглогдож байгаа өргүүд ихэнхдээ материалын тэнцүү бус байдалд явагддаг. Өрсөлдөгчдийн өөрийн хүчээ ашиглах чадваргүй байдлаас болоод өргийн туршид материалын давуу байдал нэгээс нөгөөд шилжих нь олонтоо тохиолдоно. Материалын давуу байдлаа ашиглаж сурах нь ямар ч шатарчны чадварын үндсэн бүрдүүлэгч байх ёстой. Дунд түвшингийн шатарчид багахан хэмжээний давуу байдлаа ашиглаж сурах хэрэгтэй байдаг бол эхлэн суралцагчид эхний ээлжинд их хэмжээний материалын давууг арилжиж сурах хэрэгтэй болдог.
Нээгдсэн тоо: 2534 Төлбөртэй
Өргийн төгсгөлийн гуравдугаар үед тоглох үндсэн зарчмуудтай танилцая.
Төвлөх зарчим
Шатрын тоглолтын бүх үед төвлөх зарчим үйлчилнэ. Гэхдээ төгсгөлийн үед өмнөх хоёр үеэсээ ялгаатай нь энэхүү зарчмыг бүр ноён хүртэл баримтлах хэрэгтэй. Ноёноо хэрхэн зөв ашиглахаас энэ үед их олон зүйл шийдэгдэнэ. Өөрийн шатруудыг төвд байршуулахыг тоглогч бүр хүсэх нь ойлгомжтой. Энэ нь төвийн талбайн төлөөх тэмцэлд хүргэдэг. Дараах сургамжтай жишээг авч үзье. (1-р диаграм)
Нээгдсэн тоо: 3767 Нийтийн
Ихэнх өргүүдэд үндсэн тэмцэл миттельшпиль буюу дунд хэсэгт өрнөн олон шатруудыг солилцон шатрын арми багасаж ирдэг.Үүний дараа тоглолт төгсгөлийн үе болох эндшпильд шилжинэ. Энэ үг нь Endspiel гэсэн герман үгнээс үүдэлтэй. Зарим тохиолдолд аль нэг өрсөлдөгч миттельшпильд тэр ч бүү хэл дебютэд (гараанд) бут ниргүүлэн тоглоомын төгсгөлийн үед хүрэхгүй дуусах нь байдаг. Үүнээс үндэслэн зарим нэгэн шатарчид (зөвхөн эхлэн суралцагчид ч биш) төгсгөлийн үндэс болон зарчимуудад суралцахдаа хайнга хандах нь бий. Тэдгээр хүмүүс төгсгөлийн зарчмуудыг үзэн цаг зав алдаж байснаас гарааны хувилбаруудыг сайн сурахыг илүүд үздэг. Ингэж боддог хүмүүс шатарт хэзээ ч томоохон амжилтанд хүрэхгүй. Гарааны хэдэн нүүдэлтэй хүмүүс сурсан аргаараа өрсөлдөгчөөс олж авсан хүү эсвэл бүр бодны давуу талаа хожил болгож чадахгүйд хүрдэг.





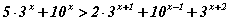 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.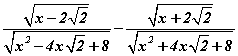 илэрхийллийн x=3 утгыг ол.
илэрхийллийн x=3 утгыг ол.